Navigation: Up Table of Contents Package Overview Bibliography Index Title

Chapter 3
Geometry Kernels

Stefan Schirra ([email protected])

The layer of geometry kernels provides basic geometric entities of constant size¹ and primitive operations on them. Each entity is provided as both a stand-alone class, which is parameterized by a kernel class, and as a type in the kernel class. Each operation in the kernel is provided via a functor class² in the kernel class and also as either a member function or a global function. See [HHK⁺01] for more details about this design. Ideally, if the kernel provides all the primitives required, you can use any kernel as a traits class directly with your algorithm or data structure; see also Chapter 4. If you need primitives not provided by the kernel (yet), please read Section 3.6 below.

3.1 Cartesian and homogeneous representation

There are two different coordinate representations available in the kernel at present: Cartesian representation and homogeneous representation. Cartesian representation is the one you are familiar with. A point in the plane is given by its x- and its y-coordinates; a point in space by its x-, y- and z-coordinates. Homogeneous representation can be seen as a divison-free representation of Cartesian coordinates. There is an additional coordinate, sometimes called the homogenizing coordinate. So with homogeneous representation in 2-space, we have coordinates (x,y,w), where w is the homogenizing coordinate, and in 3-space, we have homogeneous coordinates (x,y,z,w). Since Cgal uses homogeneous representation for affine geometry (not for projective geometry), we assume w ≠ 0. The Cartesian representation corresponding to (x₀, x₁, … , x_d, w) is (x₀/w, x₁/w, … , x_d/w). Hence, homogeneous representation is not unique; (αx,αy,αz,αw) is an alternative representation to (x,y,z,w) for any α ≠ 0. Internally, Cgal always maintains a non-negative homogenizing coordinate.

With the homogeneous representation, division operations can be avoided. Homogeneous representation is advantageous over Cartesian representation whenever systems of linear equations with integral coefficients are to be solved. By Cramer's rule, the rational solutions all have the same denominator D. The Cartesian representation would be

(N₀/D, N₁/D, … , N_d-1/D)

while a corresponding less space-consuming homogeneous representation is

(N₀, N₁, … , N_d-1, D)

For example, computing the Cartesian coordinates (x,y) of the intersection point of lines with equations a₁ X + b₁ Y + c₁ = 0 and a₂ X + b₂ Y + c₂ = 0 gives Intersection point with Cartesian coordinates

Intersection point with Cartesian coordinates

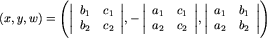
while with homogeneous representation we have Intersection point with homogeneous coordinates

In general, however, homogeneous representation is not more space-efficient. Naive conversion from a rational Cartesian represenatation

(N₀/D₀, N₁/D₁, … , N_d-1/D_d-1)

to a homogeneous representation will lead to much bigger numbers, namely,

(N₀ ∏D_i /D₀, N₁∏D_i /D₁, … , N_d-1∏D_i /D_d-1, ∏D_i )

3.2 Cartesian versus homogeneous computation

Homogeneous representation has the disadvantage that predicates become more complicated. Testing equality of points is more complicated because the homogeneous representation is not unique. In the orientation predicate, the sign of a 3x3 determinant must be computed: Orientation test with homogeneous coordinates

Orientation test with homogeneous coordinates

With Cartesian representation, it is essentially a 2x2 determinant only: Orientation test with Cartesian coordinates

With homogeneous coordinates all formulas are homogeneous polynomials in the coordinates, i.e., all monomials of homogeneous coordinates have the same total degree.³ For a sign test for some polynomial expression over Cartesian coordinates you get a corresponding sign test with an expression over homogeneous coordinates by replacing each Cartesian coordinate x_ij by hx_ij/hw_j and then multiplying by the least common multiple of the denominators, i.e., some multiple of the hw_j. Here, x_ij denotes the i-th Cartesian coordinate, hx_ij denotes the i-th homogeneous coordinate, and hw_j denotes the homogenizing coordinate of point j. Since all hw_j are positive in Cgal, sign is not affected by this multiplication.

3.3 Available kernels

At present, there are two homogeneous and two Cartesian kernels, one with reference counting (Chapter 6) and one without. The corresponding kernel classes are

CGAL::Cartesian< FieldNumberType >
CGAL::Homogeneous< RingNumberType >
CGAL::Simple_cartesian< FieldNumberType >
CGAL::Simple_homogeneous< RingNumberType >

These are all parameterized by a number type, which is used for storing the coordinates and the arithmetic in the corresponding primitives and predicates. Actually, parameterization of Homogeneous<> involves two number types. While in the internal homogeneous representation, an integral number type is sufficient, rational numbers must sometimes be used outside the internal representation, for example, when the squared length of a vector is computed. To represent such rational values, there is a second number type whose default value is CGAL::Quotient< RingNumberType >. The type of this number type can be accessed as Homogeneous<>::FT. The internally used number type can be accessed as Homogeneous<>::RT. For the sake of a uniform interface for both representations, the Cartesian kernels provide such types as well. For Cartesian representation, both FT and RT map to same number type used everywhere in the implementation of the Cartesian kernel.

Whenever one wants to ensure that predicates are evaluated correctly, an exact number type is usually necessary. As exact computations are time consuming, filtering techniques have been developed. The predicate is first evaluated using efficient but inexact floating point arithmetic. At the same time an error bound is computed that is used to judge the quality of the computed solution. If the solution is not guaranteed to be correct, the predicate is re-evaluated using exact arithmetic. The classes

CGAL::Filtered_kernel< CK >
CGAL::Filtered_kernel_adaptor< CK >

are adaptors that add such a filtering mechanism to the predicates of a given Kernel CK. Note that only predicates are affected by these adaptors, the constructions are still the same as in the original kernel CK.

The difference between Filtered_kernel and Filtered_kernel_adaptor is that the latter affects the predicate functors in the kernel only while the former also affecs the behaviour of predicates that are implemented as global functions.

3.4 Kernel design and conventions

Each kernel object is provided as both a stand-alone class, which is parameterized by a kernel class (Geo_object_D<K>), and as a type in the kernel class (K::Geo_object_D). While the former use may be more natural for users not interested in the flexibility of the kernel (and is compatable with the original kernel design [FGK⁺00]), the latter syntax should be used in all code distributed with the library as it allows types in the kernel to be easily exchanged and modified. Similarly, each operation and construction in the kernel is provided via a function object class in the kernel class and also as either a member function or a global function; developers should use the function object classes to gain access to the functionality. See [HHK⁺01] for more details about this design and how it is accomplished.

The classes for the geometric objects in the kernel have a standardized interface.

All classes have a bbox() member function computing a bounding box.
All classes have a transform(Aff_transformation_d t) member function to compute the object transformed by t.
Oriented d-1 dimensional objects⁴ provide member functions has_on_positive_side(Point_d) , has_on_boundary(Point_d) , and has_on_negative_side(Point_d) . Furthermore, there is a member function oriented_side(Point_d) returning an object of type CGAL::Oriented_side.
Full-dimensional bounded objects provide member functions has_on_bounded_side(Point_d) , has_on_boundary(Point_d) , and has_on_unbounded_side(Point_d) . Furthermore, there is a member function bounded_side(Point_d) returning an object of type CGAL::Bounded_side.
Oriented objects have a member function opposite() returning the same object with opposite orientation.

3.5 Number-type based predicates

For a number of predicates, there are versions that operate on the coordinates directly, not on the geometric objects. These number-type based predicates ease re-use with non-Cgal types.

3.6 Missing functionality

Kernel traits do not provide redundant functionality. In particular, they do not provide a right turn predicate, since a left turn predicate exists. A right turn functor can be created from the left turn functor using the function boost::bind.

Whenever you need a predicate that is not present in the current kernel traits, you should first try to re-use the available predicates (you might rewrite the code or implement the new predicate using existing ones). If this is not feasible (especially for efficiency reasons), we have to decide on adding the new predicate to the kernel traits. If the new predicate is not too special, it will be added. Otherwise you cannot use the kernel as a traits class, but have to use additional traits.

See Section 3.2 on how to derive the homogeneous version of a predicate from the Cartesian version.

Footnotes


¹	In dimension d, an entity of size O(d) is considered to be of constant size.
²	A class which defines a member operator().
³	the sum of the degrees of each variable in the monomial
⁴	Note that the dimension of an object might depend on its use. A line in the plane has dimension d-1. As a halfspace, it has dimension d.

Next chapter: Traits Classes